jueves, 9 de abril de 2015

Mayo


  • LUNES 4 DE MAYO


Funciones vectoriales

Se llama función vectorial a cualquier función de la forma
r(t) = f(t)i + g(t)j                         Plano

r(t) = f(t)i + g(t)j + h(t)k                 Espacio
Donde las funciones componentes f, g y h son funciones del parámetro t con valores reales.
Las funciones vectoriales se denotan con frecuencia de la siguiente manera:
r(t)= <f(t),g(t)>

r(t)= <f(t),g(t),h(t)>
Su dominio es el conjunto de los numeros reales y su imagen es un conjunto de vectores.
Las funciones vectoriales juegan un doble papel en la representación de curvas. Tomando como parámetro t el tiempo, las podemos usar para describir el movimiento a lo largo de una curva. Más en general, podemos usar una función vectorial para trazar la gráfica de una curva. En ambos casos, el punto final del vector posición r (t) coincide con el punto (x, y) o (x, y, z) de la curva dada por las ecuaciones paramétricas. 
Para llegar a una descripción de un campo vectorial F se considera un punto arbitrario K (x, y) y se define el vector de posición r = xi + yj de K (x, y),Se ve que F (x, y) es ortogonal a r y por lo tanto, es tangente a la circunferencia de radio ||r|| con centro en el origen. Este hecho puede demostrarse probando que r . F (x, y) = 0, como sigue:
r . F (x, y) = (xi + yj) . (- yi +xj)
= -xy + yx = 0.
Además,
|| F (x, y) || = √y2 + x2 = || r ||
Por lo tanto, la magnitud de F (x, y) es igual al radio de la circunferencia.
Esto implica que cuando el punto K (x, y) se aleja del origen, la magnitud de F (x, y) aumenta como sucede en el caso de la rueda giratoria.
Definición:
Sea r = xi + yj + zk el vector posición de un punto K (x, y, z). Se dice que un campo vectorial F es un campo de variación inversa al cuadrado de la distancia si
F(x, y, z) = c_ u
|| r ||2
donde c es un escalar y u es un vector unitario que tiene la misma dirección que r y está dado por u = 1_ = r.
|| r ||

Además se realizaron algunos ejercicios para complementar lo visto en clase.


Bibliografía:

  • http://es.aplicandofunciones.wikia.com/wiki/Funci%C3%B3n_Vectorial



  • JUEVES 7 Y JUEVES 14 DE MAYO


Complementos de las funciones vectoriales

1. Definición del Método.

Sea T ⊂ R3 una curva y sean γ : I = [a, b] → R3, γ(t) = (x(t), y(t), z(t)) una
parametrización regular y α : I′ = [a′, b′] → R3 su parametrización respecto el
parámetro arco.
A partir de la primera y segunda derivada de la parametrización de la curva
se construye el triedro de Frenet. En cada punto regular de la curva γ(t), son
tres vectores unitarios y ortonormales, T(t), B(t) y N(t). Es decir, el triedro de
Frenet es un sistema de referencia ortonormal que nos proporciona
información sobre la curva. Decimos que es un sistema de referencia móvil,
porque se desplaza por la curva según la recorremos.
Foto4.jpg
A partir de los vectores del triedro de Frenet construiremos planos (el osculador, el normal y el rectificante). También introduciremos los conceptos de curvatura y torsión, que nos darán información de cómo se “dobla” y “retuerce” la curva en el espacio.
Para llegar calcular el Triedro de Frenet en cualquier punto de una curva, lo primero que debemos hacer es parametrizarla (en el caso de que no lo este). Una vez que hallamos parametrizado la curva en cuestión, generalmente mediante coordenadas polares, podemos comenzar a “construir” nuestro Triedro de Frenet.

2. Vector Tangente.

Lo primero que deberíamos hacer es calcular el vector Tangente del triedro, ya que sobre él están basadas todos los cálculos posteriores. Para calcularlo utilizaremos la siguiente fórmula:

T=r′(t)|r′(t)|

*Donde r (t) es el vector que define a nuestra curva ya parametrizada, r’(t) es su derivada y |r’(t)| es el módulo de la derivada.

3. Vector Normal Principal.

En segundo lugar debemos calcular el vector Normal Principal del triedro, para hallar su expresión usaremos esta fórmula:

N=T′(t)|T′(t)|

*Donde T’ (t) es la derivada del vector Tangente y | T’ (t) | es el módulo de la derivada.

4. Vector Binormal.

En último lugar para completar el Triedro de Frenet, tenemos la necesidad de hallar cual es el vector Binormal, el cual es normal al Vector Tangente y al Vector Normal Principal, de ahí que podamos calcularlo mediante un simple producto vectorial entre ambos vectores:

B = T x N

5. Longitud de la curva.

Otro apartado importante, que se ve junto con el Triedro de Frenet, es como poder llegar a calcular la longitud de la curva con la que estamos trabajando.
Generalmente, usaremos la siguiente expresión:

L=∫ba|r′(t)|dt

Sin embargo, un muchas ocasiones esta integral no posee una primitiva con la cual calcular el valor de L, por lo que deberemos usar Métodos de Integración Numérica para poder aproximar el valor de L. Todos estos métodos suelen dar valores muy cercanos al verdadero, con errores inferiores al 5%.
Uno de los métodos que, personalmente, recomiendo es La Regla del Trapecio, debido principalmente a la facilidad de su uso y de su recordatorio. La cual es la siguiente:

∫baf(x)dx∼b−a2(f(a)+f(b))

Otros métodos de integración numérica son estos:

Métodos de integración numérica

6. Curvatura y Torsión.

Otra de las cosas que veremos en este apartado de la asignatura de Cálculo II, es la curvatura, así como el radio de curvatura, y también la torsión, todas ellas características propias de la curva que estamos estudiando.

6.1. Curvatura, radio de curvatura y círculo osculador.

La curvatura es una medida del cambio de dirección del vector tangente a una curva, cuanto más rápido cambia éste a medida que nos desplazamos a lo largo de la curva, se dice, que más grande es la curvatura. Su expresión es:

K=T′(t)|r′(t)|

De esta misma manera, definimos el radio de curvatura como la magnitud que mide la curvatura de un objeto geométrico, tal como una línea curva, una superficie o ,más en general, una variedad diferenciable definida en un espacio euclídeo. Su expresión es:

ρ=1K

En este apartado, además veremos el círculo osculador, que por así decirlo es el que “besa” a la curva en un punto dado. Una definición un poco más técnica sería esta: es una circunferencia cuyo centro se encuentra sobre la normal a la curva y tiene la misma curvatura que la curva dada en ese punto. El centro y el radio de la circunferencia osculatriz, en un punto de la curva, son llamados centro de curvatura y radio de curvatura de la curva en ese punto. El plano en el que está contenida la circunferencia osculatriz se denomina plano osculador.
foto5.jpg *Donde el radio de curvatura es ρ.

6.2. Torsión.

La torsión es una medida del cambio de dirección del vector binormal: cuanto más rápido cambia la torsión, más rápido gira el vector binormal alrededor del vector tangente y más retorcida aparece la curva. Por lo tanto, para una curva totalmente contenida en el plano, la torsión es nula, ya que, el vector binormal es constantemente perpendicular al plano que la contiene. Su expresión es:

τ=−N∗dBds=−T′(t)|T′(t)|∗T(t)∗N′(t)|r′(t)|

 Foto6.jpg

7. Planos del Triedro de Frenet.

Por último, en este apartado de la asignatura, debemos aprender a calcular y a dominar los conceptos de plano Normal, Rectificante y Osculador.
Foto7.jpg
Como podemos ver en la imagen el Plano Normal es perpendicular al Vector Tangente, el Plano Rectificante es perpendicular al Vector Normal Principal y el Plano Osculador es normal al Vector Binormal. Sus expresiones son:

Plano Normal.




(X−r(t))∗T=0

Plano Rectificante.

(X−r(t))∗N=0

Plano Osculador.

(X−r(t))∗B=0


Bibliografía:

  • http://matcalculus.wikidot.com/frenet




  • LUNES 25 DE MAYO


Se realizaron algunos ejercicios para complementar lo aprendido en clase sobre las funciones vectoriales realizando métodos analíticos, gráficos y descriptivos.

Curvas de nivel

De la misma forma que una función de una variable tiene una representación gráfica mediante una curva en el plano, cuando la función tiene dos variables podría representarse mediante una superficie en el espacio tridimensional. Dicha superficie estaría formada por los puntos de la forma (X, Y, f (X,Y)). No obstante, existe una forma de representar gráficamente funciones de dos variables en el plano: mediante las conocidas como curvas de nivel de la función. Dichas curvas se obtienen al cortar la superficie mediante planos horizontales a distintas alturas, de forma que todos esos cortes forman una familia de curvas que se proyectan sobre el plano OXY. Las curvas de nivel surgen por ejemplo en cartografía cuando se representan las distintas altitudes de una montaña mediante un conjunto de curvas; de esta forma se hace una representación en el plano de la superficie tridimensional de la montaña. En meteorología, las isobaras no son más que las curvas de nivel de la función que determina la presión atmosférica; es decir, son las curvas formadas por los puntos de igual presión atmosférica.
La siguiente figura muestra la representación gráfica de la función sen(X Y) mediante su superficie en el espacio y sus curvas de nivel en el plano.
Definición:

Las curvas de nivel de la función f (X,Y) son la familia de curvas de la forma: f (X,Y) = k para cada valor de k en R. Ejemplo:
Este ejemplo muestra la construcción de la familia de curvas de nivel de la función f (X,Y) = 3 X – Y.
Las curvas de nivel tienen la forma 3 X – Y = k o si se prefiere Y = 3 X – K, por tanto, son una familia de rectas paralelas como muestra la figura.
En el caso de funciones lineales, las curvas de nivel son siempre una familia de rectas paralelas.

Curvas y superficies de nivel más usadas:

Circunferencia con centro en (h,j) y radio r: 

(x-h)^2+(y-j)^2=r^2 


graficos 

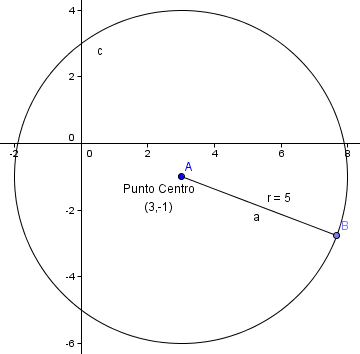
Elipse con centro en (h,j) y semiejes a y b: 
((x-h)^2)/a^2+((y-j)^2)/b^2=1 
esfera 

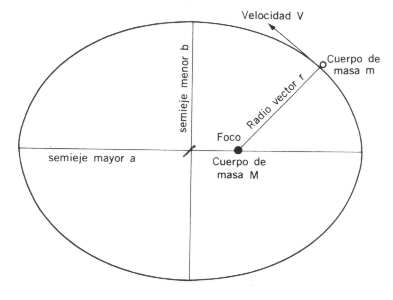
Paraboloide: 

f(x,y)=x^2+y^2 si despejo z me queda 0=x^2+y^2-z 

Nivel 

Paraboloide hiperbolico, o silla de montar: 

f(x,y)=x^2-y^2 despejo z entonces me queda 0=x^2+y^2-z 
curvas 

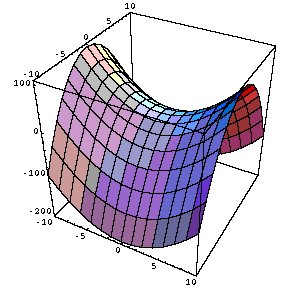
Hiperboloide de una hoja de revolución: 

1=x^2+y^2-z^2 

elipse 


Hiperboloides de 2 hojas: 

-1=x^2+y^2-z^2 
circunferencia 


Esfera: 

radio^2=x^2+y^2+z^2 


paraboloide

Elipsoide: 

1= (x^2)/a^2 + (y^2)/b^2 +(z^2)/c^2 

elipsoide 

Límites y continuidad

Funciones de varias variables

Vamos a considerar funciones de $\mathbb{R}^n$ en $\mathbb{R}^m$, $f\colon\mathbb{R}^n\to\mathbb{R}^m$. Distinguimos algunos tipos de funciones:
Si $n=m=1$ hablamos de funciones reales de variable real o funciones de una variable, que son las que hemos estudiado hasta ahora, $f\colon\mathbb{R}\to \mathbb{R}$.
Si $f\colon\mathbb{R}\to \mathbb{R}^m$ se dice que es una función vectorial.
Si $f\colon\mathbb{R}^n \to \mathbb{R}$ se dice que es un campo escalar.
En general si $f\colon\mathbb{R}^n\to\mathbb{R}^m$ decimos que es un campo vectorial.
Para funciones $f\colon\mathbb{R}^n\to\mathbb{R}^m$ se definen los conceptos de Dominio, Imagen y Gráfica:
Dominio de $f =\{x\in \mathbb{R}^n /\quad f(x) \mbox{ existe }\}\subset \mathbb{R}^n$
Imagen de $f =\{y\in \mathbb{R}^m /\quad y=f(x), \mbox{ para algún } x\}\subset \mathbb{R}^m$
Gráfica de $f =\{(x, f(x)) /\quad x\in \mbox{ Dom } f\}\subset \mathbb{R}^n\times\mathbb{R}^m$

Límites en funciones vectoriales

La definición de límite es análoga a la del caso real y la generaliza. Dada una función vectorial, $f\colon I\to \mathbb{R}^m$, $a\in I\subset \mathbb{R}$ un punto de acumulación (es decir, que hay puntos del dominio tan cerca de $a$ como queramos), y $v\in\mathbb{R}^m$, decimos que $v$ es el límite de $f$ cuando $t$ tiende a $a$, ${\displaystyle \lim_{t\to a}f(t)=v }$, si ocurre que 

\begin{displaymath}\forall \epsilon >0, \exists \delta >0\mbox{ tal que } \mid \mid f(t)-v \mid \mid <\epsilon\mbox{ si }0< \mid t-a \mid <\delta\end{displaymath}
Como la norma en el caso $\mathbb{R}^m=\mathbb{R}$ coincide con el valor absoluto, esta definición generaliza a la que conocemos de $\mathbb{R}$ en $\mathbb{R}$. 

Continuidad de funciones vectoriales

La continuidad se define como en el caso de una variable. Si $a$ es del dominio de $f$, $f\colon\mathbb{R}\to \mathbb{R}^m$, $f$ se dice que es continua en $x=a$ si ocurre que existe ${\displaystyle \lim_{t\to a}f(t) }$ y coincide con $f(a)$, 

\begin{displaymath}\lim_{t\to a}f(t)=f(a)\end{displaymath}
Como nos podemos reducir a las funciones componentes, resulta que $f$ es continua en $a$ si y solo si cada función componente $f_i$ es continua en $a$. 

\begin{displaymath}f(a)=(f_1(a),f_2(a),\cdots ,f_m(a))\in \mathbb{R}^m\end{displaymath}


\begin{displaymath}\lim_{t\to a}f(t)=f(a)\iff \lim_{t\to a}f_i(t)=f_i(a) ,\quad i=1,2,\cdots , m\end{displaymath}

Definición(límite de un campo escalar):

Sea $f\colon\mathbb{R}^n \to \mathbb{R}$ un campo escalar, y sea $a$ un punto de acumulación del dominio $D$ de $f$ y $l\in \mathbb{R}$. Decimos que $l$ es el límite de $f$ cuando $x$ tiende a $a$ si ocurre que 

\begin{displaymath}\forall \epsilon >0, \exists \delta >0\mbox{ tal que si } \mi... ...\mid \mid <\delta, \mbox{ entonces } \mid f(x)-l \mid <\epsilon\end{displaymath}

$x\in D$
$x\neq a$
En este caso escribimos 

\begin{displaymath}\lim_{x\to a}f(x)=l\end{displaymath}

Definición(Continuidad de campos escalares):

Un campo escalar $f\colon\mathbb{R}^n \to \mathbb{R}$ es continuo en $a$ si ocurre que 
\begin{displaymath}\lim_{x\to a}f(x)=f(a)\end{displaymath}


Como vemos las definiciones son iguales, con la salvedad que si tenemos vectores medimos con la norma en lugar de con el valor absoluto, y que en este caso $x$ y $a$ son vectores de $\mathbb{R}^n$ y $f(x)$ y $f(a)$ son números, 

\begin{displaymath}x=(x_1,x_2,\cdots , x_n),\quad a=(a_1,a_2,\cdots , a_n),\qquad f(x), f(a)\in \mathbb{R}\end{displaymath}


Para campos vectoriales todo se repite de forma análoga 

Campos vectoriales

Sea $f\colon\mathbb{R}^n\to\mathbb{R}^m$ un campo vectorial. Sea $a$ punto de acumulación del dominio $D$ de $f$ y $v\in\mathbb{R}^m$. 
\begin{displaymath}\lim_{x\to a}f(x)=v\iff\forall \epsilon >0, \exists \delta >0... ... \mid <\delta, \Rightarrow \mid \mid f(x)-v \mid \mid <\epsilon\end{displaymath}


$x\in D$ $x\neq a$Un campo vectorial $f\colon\mathbb{R}^n\to\mathbb{R}^m$ es continuo en $x=a$ si ocurre que 

\begin{displaymath}\lim_{x\to a}f(x)=f(a)\end{displaymath}


Ahora $x,a\in \mathbb{R}^n$ y $f(x),f(a)\in \mathbb{R}^m$.
El principal resultado que relaciona límites y continuidad de campos vectoriales con campos escalares, es el siguiente: 

Resultado

$f\colon\mathbb{R}^n\to\mathbb{R}^m$, $f=(f_1,f_2,\cdots ,f_m)$, $f_i\colon\mathbb{R}^n\to \mathbb{R}$ $i=1,2,\cdots , m$
  • ${\displaystyle \lim_{x\to a}f(x)=v=(v_1,\cdots , v_m)\iff \lim_{x\to a}f_i(x)=v_i \, i=1,\cdots , m }$
  • $f\colon\mathbb{R}^n\to\mathbb{R}^m$ es continuo en $x=a$ $\iff$ para cada $i=1,\cdots , m$ $f_i\colon\mathbb{R}^n\to \mathbb{R}$ es continuo en $x=a$.
Además se pudo revisar un poco acerca de las derivadas implícitas con lo cual se acabó esta clase.


Bibliografía:
  • http://www.virtual.unal.edu.co/cursos/sedes/manizales/4060014/html/Capitulo%20I/curvas.htm
  • http://www.taringa.net/post/ciencia-educacion/15569293/Superficies-y-curvas-de-nivel-formulas-y-graficos.html
  • http://www.matap.uma.es/~garvin/05Ca11/index.html

Publicado por en
Etiquetas:

7 comentarios:

Suscribirse a: Enviar comentarios (Atom)