- LUNES 7 DE ABRIL
Primera Clase:
La ingeniera dio una introducción acerca de la plataforma virtual a usarse durante este semestre, la misma que nos servirá para revisar, subir, estudiar y muchas más utilidades para nuestro conocimiento acerca de la materia.
- JUEVES 9 DE ABRIL
Geometría en el Espacio
Rama de la geometría que se ocupa de las propiedades y medidas de figuras geométricas en el espacio tridimensional. Entre estas figuras, también llamadas sólidos, se encuentran el cono, el cubo, el cilindro, la pirámide, la esfera y el prisma. La geometría del espacio amplía y refuerza las proposiciones de la geometría plana, y es la base fundamental de la trigonometría esférica, la geometría analítica del espacio, la geometría descriptiva y otras ramas de las matemáticas. Se usa ampliamente en matemáticas, en ingeniería y en ciencias naturales.
PUNTO :
Es la marca que deja un lápiz sobre una hoja, la intersección de dos rectas, etc.
PLANO:
Una porción de espacio.
RECTA:
Línea que pasa por dos puntos cualesquiera.
Sistema de Funciones Implícitas
f (x,y) = 0
g (x,y) = 0
g (x,y) = 0
OBS: Cada función representa una curva en R2, la intersección de 2 o mas curvas genera uno o mas puntos
R3 F(X,Y,Z) = 0 Función implícita de 3 variables
i) x = f(y,z) --- x: valor dependiente; y,z: variables independientes.
ii) y = g(x,z) --- y: valor dependiente; x,z variables independientes.
iii) z = h(x,y) --- z: valor dependiente; x,y: variables independientes.
f(x,y) = 0 Superficie cilíndrica de generatriz paralela al eje oz
La recta en el espacio








Ecuación vectorial de la recta
Sea P(x1, y1) es un punto de la recta r y  su vector director, el vector
su vector director, el vector  tiene igual dirección
tiene igual dirección
que  , luego es igual a
, luego es igual a  multiplicado por un escalar:
multiplicado por un escalar:




Ecuaciones paramétricas de la recta
Operando en la ecuación vectorial de la recta llegamos a la igualdad:

Esta igualdad se verifica si:

Ecuaciones continuas de la recta
Despejando e igualando λ en las ecuaciones paramétricas se tiene:

Ecuaciones implícitas de la recta
Una recta puede venir determinada por la intersección de los planos.

Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas.
Bibliografía:
- http://html.rincondelvago.com/geometria-del-espacio.html
- http://www.vitutor.com/analitica/recta/ecuaciones_recta.html
- LUNES 13 DE ABRIL
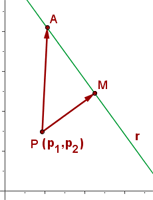
Distancia de un punto a una recta
La distancia de un punto, P, a una recta, r, es la menor de la distancia desde el punto a los infinitos puntos de la recta.
Esta distancia corresponde a la perpendicular trazada desde el punto hasta la recta.
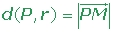
Distancia entre dos rectas
La distancia entre dos rectas r y r′ , d(r,r′) , es la mínima distancia entre un punto cualquiera de r y un punto cualquiera de r′ .
- Si las rectas son coincidentes o secantes, la distancia entre ellas es cero,
d(r,r′)=0 . - Si las rectas son paralelas, se calcula la distancia entre ellas tomando un punto cualquiera de una de las dos rectas,
P∈r oP′∈r′ , y encontrando la distancia a la otra recta:d(r,r′)=d(P,r′)=d(r,P′) - Si las rectas se cruzan, se deduce la siguiente fórmula general para calcular la distancia entre ellas:Tomamos un punto
A perteneciente ar y otro puntoA′ perteneciente ar′ . Seanv⃗ yv⃗ ′ vectores directores der yr′ . Unimos los puntosA yA′ . El volumen del paralelepípedo determinado porAA′−→−− ,v⃗ yv⃗ ′ , es el valor absoluto del producto mixto de estos vectores:vp=|[AA′−→−−,v⃗ ,v⃗ ′]|
Por otro lado también podemos calcular este volumen mediante el producto del área de la base por la altura:vp=|v⃗ ×v⃗ ′|d(r,r′)|
Por tanto:d(r,r′)=|[AA′−→−−,v⃗ ,v⃗ ′]||v⃗ ×v⃗ ′|
Ecuación del plano
Un plano del espacio queda determinado cuando conocemos un punto P del mismo y dos vectores u y v, no nulos y linealmente independientes contenidos en el plano, llamados vectores directores del mismo.
Sea un plano π que tiene como vectores directores u=(u1,u2,u3), v=(v1,v2,v3) y pasa por un punto P0(x0,y0,z0), si P(x,y,z) es un punto cualquiera del plano: OP=OP0+tu+sv.
Sea un plano π que tiene como vectores directores u=(u1,u2,u3), v=(v1,v2,v3) y pasa por un punto P0(x0,y0,z0), si P(x,y,z) es un punto cualquiera del plano: OP=OP0+tu+sv.
|
(x,y,z)=(x0,y0,z0)+t·(u1,u2,u3)+s·(v1,v2,v3)
|
ECUACIÓN
VECTORIAL |
|
x=x0+t·u1+s·v1
y=y0+t·u2+s·v2 z=z0+t·u3+s·v3 | ECUACIONES PARAMÉTRICAS |
|  desarrollando: Ax+By+Cz=D | ECUACIÓN GENERAL |
|
A·(x-x0)+B·(y-y0)+C·(z-z0)=0
| ECUACIÓN NORMAL |
Bibliografía:
- http://www.ditutor.com/distancias/dpr.html
- http://www.catedu.es/matematicas_blecua/bacmat/temario/bac2/mat2_06rectasyplanos_t2.htm
- JUEVES 16 DE ABRIL
Ecuación segmentaria
En este caso, el plano corta a los 3 ejes.
La intersección del plano con cada uno de los ejes nos da el valor de las coordenadas de cada punto.
Podemos tratar a esta forma como un caso particular de la ecuación del plano cuando conocemos tres puntos.
En la figura siguiente tenemos representado este plano que corta a los tres ejes:
La intersección del plano con cada uno de los ejes nos da el valor de las coordenadas de cada punto.
Podemos tratar a esta forma como un caso particular de la ecuación del plano cuando conocemos tres puntos.
En la figura siguiente tenemos representado este plano que corta a los tres ejes:
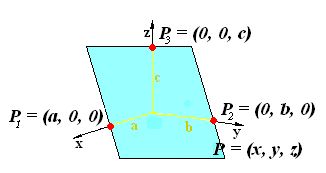
Como vemos en la figura, el plano corta a los ejes en los puntos:
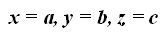
El punto P es uno cualquiera del plano cuyas coordenadas son: 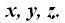
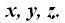
El resto de los valores los obtenemos de:
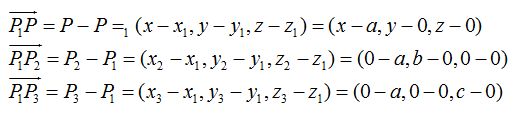
Para calcular la ecuación hacemos uso de lo estudiado en la ecuación del plano cuando conocemos tres puntos:
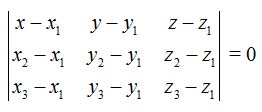
Sustituimos los valores de las nuevas coordenadas:
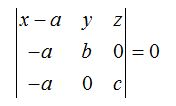
Resolvemos el determinante:
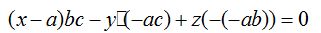
Hacemos operaciones:
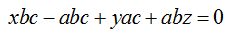
Dividimos cada término por abc:
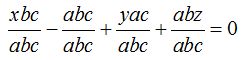
Simplificamos:
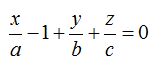
Pasamos el 1al segundo miembro de la igualdad y obtenemos la ecuación del plano en la forma segmentaria:
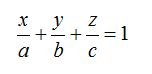
Ecuación normal del plano
Datos:
n = ( cosα; cosβ; cosγ)
P = proyección el vector normal P = proy(r/n)
pd: Ec. Normal del plano
P = proy (B/A) = Bcosθ
A.B = A.Bcosθ
A.B = A.p
P = (A.B/A)
P = ( cosα, cosβ, cosγ).(x,y,z)
P = xcosα + ycosβ + zcosγ
Distancia de un punto a un plano
La distancia de un punto, P, a un plano, π, es la menor de la distancia desde
el punto a los infinitos puntos del plano.
Esta distancia corresponde a la perpendicular trazada desde el punto al plano.
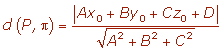

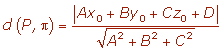
Bibliografía:
- http://www.aulafacil.com/cursos/l10896/ciencia/matematicas/planos-en-el-espacio/ecuacion-segmentaria
- http://www.ditutor.com/distancias/punto_plano.html
- LUNES 20 DE ABRIL
Ecuación del plano dado tres puntos
Tenemos un plano que pasa por los puntos cuyas componentes son, respectivamente:
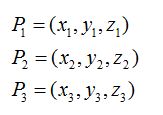
Los vectores representamos en la figura siguiente:
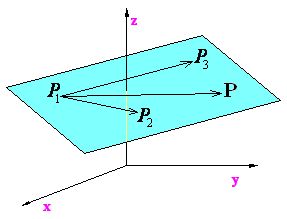
Un punto cualquiera del plano lo representamos con P, cuyas componentes desconocidas son: 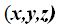
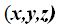
Sabemos que dos puntos determinan un vector, por ejemplo, el
vector:
vector:
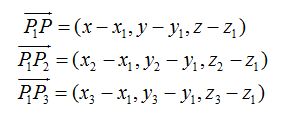
Hemos estudiado que la forma implícita de la ecuación del plano es:

Si a las componentes de los vectores 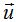 y
y 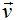 los sustituimos por las componentes de cada uno de los tres puntos del plano que conocemos, obtenemos:
los sustituimos por las componentes de cada uno de los tres puntos del plano que conocemos, obtenemos:
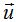 y
y 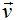 los sustituimos por las componentes de cada uno de los tres puntos del plano que conocemos, obtenemos:
los sustituimos por las componentes de cada uno de los tres puntos del plano que conocemos, obtenemos: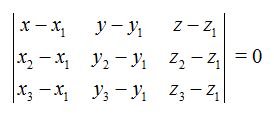

Si r viene definida por sus ecuaciones implícitas:

la ecuación del haz de planos de eje r viene dada por la igualdad:

Si dividimos por λ y hacemos  , la ecuación del haz resulta:
, la ecuación del haz resulta:
Ecuación vectorial de la esfera , la ecuación del haz resulta:
, la ecuación del haz resulta:
En un sistema de coordenadas cartesianas en un espacio euclidiano tridimensional, la ecuación de la esfera unitaria (de radio 1), con centro en el origen, es:
Esta ecuación se obtiene considerando que en el punto M (x, y, z) de la esfera, el vector normal OM es igual a 1.
Generalizando, la esfera de radio r, de centro Ω (a, b, c) tiene como ecuación:
Bibliografía:
- http://www.aulafacil.com/cursos/l10895/ciencia/matematicas/planos-en-el-espacio/ecuacion-del-plano-que-pasa-por-tres-puntos
- http://www.vitutor.com/analitica/recta/haces_planos.html
- http://es.wikipedia.org/wiki/Esfera
- JUEVES 23 DE ABRIL
Superficies de segunda orden (análisis de gráficos)
I) Intersección con ejes coordenados
II) Intersección con planos coordenados
III) Intersección con planos paralelos
Ejemplo: Realice el análisis grafico de X^2 + Y^2 = Z
I) Intersección con ejes coordenados

II) Intersección con planos coordenados

III) Intersección con planos paralelos

Después de los planos, las superficies mas sencillas son las definidas por ecuaciones de segundo grado en coordenadas cartesianas, llamadas superficies de segundo orden o cuádricas.
Elipsoide.- Llamamos elipsoide a la superficie que en un sistema cartesiano de coordenadas se determina por la ecuación:


Las secciones del elipsoide por planos paralelos a los planos coordenados son elipses.
En el caso particular de que alguno de los parámetros a, b, c se repita, las secciones elípticas se convierten en circunferencias y puede considerarse el elipsoide como engendrado por la rotación de la elipse alrededor de uno. de los ejes. En este último caso el elipsoide se llama entonces de revolución.
Si coinciden los tres parámetros a = b = c, nos encontramos con el caso de una esfera. La ecuación :

no determina ninguna figura real, pero por analogía con la ecuación anterior, recibe el nombre de ecuación del elipsoide imaginario
Hiperboloide de una hoja.- Llamamos hiperboloide de una hoja a la superficie que en un sistema cartesiano de coordenadas se determina por la ecuación:


Los parámetros a, b, c son los semiejes del hperboloide de una hoja. Si seccionamos la figura por planos paralelos al XOY, las secciones son elipses semejantes.
La elipse determinada por el plano XOY es la menor de todas las posibles y recibe el nombre de elipse de garganta. Si desarrollamos una sección por un plano que contenga al eje Z, se obtiene una hipérbola. En el caso de que coincidan dos de los parámetros, a = b, las secciones por planos paralelos al XOY son circunferencias con centro en el eje OZ. Podemos considerar en este caso que el hiperboloide está engendrado por la rotación de una hipérbola alrededor de uno de sus ejes.
Hiperboloide de dos hojas.- llamamos hiperboloide de dos hojas a la superficie que en un sistema de coordenadas cartesianas se determina por la ecuación:


que representa un hiperboloide de dos hojas sobre el eje Z.
Cuando el signo negativo antecede a cualquiera de los otros dos términos, el hiperboloide se encuentra sobre el eje coordenado que afecta. Paraboloide elíptico.- Llamamos paraboloide elíptico a la superficie que en un sistema cartesiano de coordenadas se determina por la ecuación:


el punto que coincide con el origen de coordenadas se llama vértice del paraboloide. Puede ocurrir que la figura no coincida con el origen de coordenadas en el vértice; la ecuación toma entonces la forma:

Las secciones que se obtienen al cortar la figura por planos que contienen al eje OZ son parábolas y las que se obtienen al cortarla por planos que contengan al eje YO son elipses.
Paraboloide hiperbólico.- Llamamos paraboloide hiperbólico a la superficie que en un sistema rectangular de coordenadas se determina por la ecuación :

Esta figura se conoce con el nombre de silla de montar. Cuando la ecuación anterior toma la forma dada por la ecuación


Elipsoide.- Llamamos elipsoide a la superficie que en un sistema cartesiano de coordenadas se determina por la ecuación:


Las secciones del elipsoide por planos paralelos a los planos coordenados son elipses.
En el caso particular de que alguno de los parámetros a, b, c se repita, las secciones elípticas se convierten en circunferencias y puede considerarse el elipsoide como engendrado por la rotación de la elipse alrededor de uno. de los ejes. En este último caso el elipsoide se llama entonces de revolución.
Si coinciden los tres parámetros a = b = c, nos encontramos con el caso de una esfera. La ecuación :

no determina ninguna figura real, pero por analogía con la ecuación anterior, recibe el nombre de ecuación del elipsoide imaginario
Hiperboloide de una hoja.- Llamamos hiperboloide de una hoja a la superficie que en un sistema cartesiano de coordenadas se determina por la ecuación:


Los parámetros a, b, c son los semiejes del hperboloide de una hoja. Si seccionamos la figura por planos paralelos al XOY, las secciones son elipses semejantes.
La elipse determinada por el plano XOY es la menor de todas las posibles y recibe el nombre de elipse de garganta. Si desarrollamos una sección por un plano que contenga al eje Z, se obtiene una hipérbola. En el caso de que coincidan dos de los parámetros, a = b, las secciones por planos paralelos al XOY son circunferencias con centro en el eje OZ. Podemos considerar en este caso que el hiperboloide está engendrado por la rotación de una hipérbola alrededor de uno de sus ejes.
Hiperboloide de dos hojas.- llamamos hiperboloide de dos hojas a la superficie que en un sistema de coordenadas cartesianas se determina por la ecuación:


que representa un hiperboloide de dos hojas sobre el eje Z.
Cuando el signo negativo antecede a cualquiera de los otros dos términos, el hiperboloide se encuentra sobre el eje coordenado que afecta. Paraboloide elíptico.- Llamamos paraboloide elíptico a la superficie que en un sistema cartesiano de coordenadas se determina por la ecuación:


el punto que coincide con el origen de coordenadas se llama vértice del paraboloide. Puede ocurrir que la figura no coincida con el origen de coordenadas en el vértice; la ecuación toma entonces la forma:

Las secciones que se obtienen al cortar la figura por planos que contienen al eje OZ son parábolas y las que se obtienen al cortarla por planos que contengan al eje YO son elipses.
Paraboloide hiperbólico.- Llamamos paraboloide hiperbólico a la superficie que en un sistema rectangular de coordenadas se determina por la ecuación :

Esta figura se conoce con el nombre de silla de montar. Cuando la ecuación anterior toma la forma dada por la ecuación


la figura queda invertida.
Una cuádrica se llama degenerada cuando tiene por lo menos un punto singular. Un punto singular de una cuádrica es aquél para el que se anulan todos los coeficientes de la ecuación del plano tangente en dicho punto. Se tiene que si se anulan los coeficientes, toda recta que pase por dicho punto es tangente y, por lo tanto, no se puede hablar de plano tangente en dicho punto.
Una cuádrica degenerada pertenece, según tenga un punto singular propio o impropio a uno u otro (o ambos) de los dos tipos siguientes:
Conos cuádricos.- Llamamos cono cuádrico o cono de segundo orden a la superficie que en un sistema de coordenadas cartesianas se determina por cualquiera de las ecuaciones:
Una cuádrica se llama degenerada cuando tiene por lo menos un punto singular. Un punto singular de una cuádrica es aquél para el que se anulan todos los coeficientes de la ecuación del plano tangente en dicho punto. Se tiene que si se anulan los coeficientes, toda recta que pase por dicho punto es tangente y, por lo tanto, no se puede hablar de plano tangente en dicho punto.
Una cuádrica degenerada pertenece, según tenga un punto singular propio o impropio a uno u otro (o ambos) de los dos tipos siguientes:
Conos cuádricos.- Llamamos cono cuádrico o cono de segundo orden a la superficie que en un sistema de coordenadas cartesianas se determina por cualquiera de las ecuaciones:
 ;
;  ;
; 



La ecuación :

determina un punto real único que es el (0,0,0) y recibe el nombre de ecuación del cono imaginario.
El punto singular del cono cuádrico es su vértice.
Cilindros cuádricos.- Podemos considerar varios tipos de cilindros cuádricos según que sus secciones paralelas al plano generatriz sean elipses, hipérbolas o parábolas.
En el primer caso tenemos el cilindro elíptico dado por la ecuación de la izquierda:



En el segundo caso se tiene el cilindro hiperbólico dado por ecuación de la derecha y en el tercer caso se obtiene el cilindro parabólico dado por cualquiera de las ecuaciones:

determina un punto real único que es el (0,0,0) y recibe el nombre de ecuación del cono imaginario.
El punto singular del cono cuádrico es su vértice.
Cilindros cuádricos.- Podemos considerar varios tipos de cilindros cuádricos según que sus secciones paralelas al plano generatriz sean elipses, hipérbolas o parábolas.
En el primer caso tenemos el cilindro elíptico dado por la ecuación de la izquierda:



En el segundo caso se tiene el cilindro hiperbólico dado por ecuación de la derecha y en el tercer caso se obtiene el cilindro parabólico dado por cualquiera de las ecuaciones:
Bibliografía:
- http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm




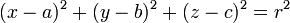


No hay comentarios:
Publicar un comentario