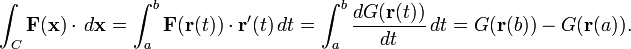CÁLCULO VECTORIAL: 2015

LUNES 1 DE JUNIO

Diferenciales e incrementos diferenciales

Para funciones de una variable $\,y = f(x)\,$ , se define el incremento de $\,y\,$ como

$\begin{displaymath}\Delta y \, = \, f(x + \Delta x) - f(x) \end{displaymath}$

y la diferencial de $\,y\,$ como

$\begin{displaymath}dy\,=\,f'(x)dx\end{displaymath}$

$\,\Delta y\,$ representa el cambio en la altura de la curva $\,y\,=\,f(x)\,$ y $\,dy\,$ representa la variación en $\,y\,$ a lo largo de la recta tangente cuando $\,x\,$ varía en una cantidad $\,dx\,=\, \Delta x\,$ .

En la siguiente figura se muestra $\,df\, \, \mbox{y} \, \, \Delta f\,$ .

Figura 1: diferencial

Observe que $\,\Delta y - dy\,$ se aproxima a cero más rápidamente que $\,\Delta x\,$ , ya que

$\,\displaystyle{\epsilon\,= \, \frac{\Delta y - dy}{\Delta x}\, = \, \frac{f(x ... ...x)\Delta x}{\Delta x}\, = \, \frac{f(x + \Delta x) - f(x)}{\Delta x} - f'(x)}\,$

y al hacer $\,\Delta x \longrightarrow 0\,$ , tenemos que $\,\epsilon \longrightarrow 0\,$ .

Por tanto

$\begin{displaymath}\Delta y \, = \, dy + \epsilon\, \Delta x\end{displaymath}$

donde $\,\epsilon \longrightarrow 0\,$ conforme $\,\Delta x \longrightarrow 0\,$ .

Ahora consideremos una función de dos variables $\,z\, = \, f(x, y)\,$ .

Si $\,x\,$ y $\,y\,$ son incrementados $\,\Delta x\,$ y $\,\Delta y\,$ , entonces el correspondiente incremento de $\,z\,$ es

$\begin{displaymath}\Delta z\, = \, f(x + \Delta x, y + \Delta y) - f(x, y)\end{displaymath}$

Con lo cual $\,\Delta z\,$ representa el cambio en el valor de $\,f\,$ cuando $\,(x, y)\,$ cambia a $\,(x + \Delta x, \; y + \Delta y)\,$ .

	Definición
	Sean $\,f :\,D \subset \mathbb{R}^{2}\, \longrightarrow \mathbb{R}\,$ una función escalar y $\,\Delta x\,$ y $\,\Delta y\,$ incrementos de $\,x\,$ y de $\,y\,$ , entonces la diferencial total de la variable dependiente $\,z\,$ es $\begin{displaymath}dz\, = \, f_{x}(x, y)\Delta x + f_{y}(x, y)\Delta y\end{displaymath}$

Bibliografía:

http://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/SUPERIOR/t5-Incrementos-diferenciales/node1.html

JUEVES 4 DE JUNIO

Derivación de funciones compuestas

Sea

donde

Entonces la derivada de la función compuesta

se puede calcular: o bien haciendo la sustitución, o bien, aplicando la siguiente fórmula:

, donde

, entonces la derivada total de z respecto de x se puede calcular: o bien haciendo la sustitución, o bien, aplicando la siguiente fórmula:

, donde

entonces las derivadas parciales se pueden calcular mediante las siguientes fórmula:

Derivadas de orden superior

Como la derivada de una función es otra función, entonces podemos tratar de hallar su derivada. Si hacemos tal cosa, el resultado es de nuevo una función que pudiera ser a su vez derivada. Si continuamos así una y otra vez, tenemos lo que se conoce por derivadas de orden superior.

Por ejemplo, si f(x) = 6x³ - 5x², entonces la:

primera derivada es : f’(x) = 18x² - 10x

segunda derivada es: f"(x) = 36x - 10

tercera derivada es : f’’’(x) = 36

cuarta derivada es : f⁽⁴⁾(x) = 0

n-ésima derivada es : f⁽ⁿ⁾ (x) = 0

Ejemplos para discusión:

1) Si f(x) = -x⁴ + 2x³ + x + 4, halla f’’’(-1).

2) Halla las primeras cuatro derivadas de :

Nota: Si f’(x) representa la pendiente de la gráfica de f, entonces f"(x) representa la pendiente de la gráfica de f’. Así también, f’’’(x) representa la pendiente de la gráfica de f".

Bibliografía:

http://www.matap.uma.es/~svera/probres/pr3/pr3_5.html
http://facultad.bayamon.inter.edu/ntoro/derivadasfunalgebraicas.htm

LUNES 8 DE JUNIO

Derivación de funciones implícitas

Función implícita de una variable.

Sea una ecuación con 2 indeterminadas, en la forma F(x, y) = 0, se dice que esta ecuación define en el entorno de un punto Po a y=f(x) como una función implícita de una variable, si para todo punto P del entorno de Po se tiene que: F(x, f(x))º 0.

Por ejemplo, la ecuación de la circunferencia x² + y² – 1 = 0, define en el entorno del punto

la función implícita :

Una función que al sustituir en la ecuación la convierte en una identidad del tipo 0º0.

De la misma manera en el entorno del punto

, la misma ecuación define otra función implícita:

* Teoréma de existencia y unicidad:

Sea una ecuación de dos variables F(x,y) = 0 {1}, esta ecuación define una función implícita y = f(x) en el entorno de cierto punto

si se cumplen las tres condiciones:

, es decir, el punto Po es un punto de la curva.

b) Las dos derivadas parciales

son funciones contínuas en cierto entorno del punto Po.

En este caso podemos hallar la derivada primera de la función implícita de la siguiente manera. Primero diferenciamos ambos miembros de la ecuación F(x,y) = 0.

{2}

A continuación, despejamos dy:

Por lo tanto, la derivada de la función implícita y = f(x) es:

{3}

(obsérve cómo hemos cálculado la derivada de la función y=f(x) sin necesidad de conocer la forma explícita de ésta, una forma que quizás no podemos saber por ser imposible depejar "y" de la ecuación {1} )

O también, expresada en forma más simple:

{3'}

Es necesario hacer notar que la expresión {3} no tiene una validez general, sino que sólo es válida para los puntos de un entorno de Po .

Una vez hallada la primera derivada, las derivadas sucesivas las obtenemos a base de ir derivando ésta, aunque hay que tener en cuenta en todo momento que la "y" es una función de x.

Ejemplo: Supongamos la ecuación siguiente:

Es obvio que en esta ecuación no podemos despejar "y" (y se encuentra en forma implícita), no obstante, nos piden que estudiemos el comportamiento de la función y = y(x) en las proximidades del punto P(1,0).

Solución: Para hacer este estudio local de y = y(x), vamos a calcular las derivadas y' , y", en un entorno del punto P(1,0).

Para tener la ecuación en la forma {1}, debemos tomar:

y en esta función F(x,y) realizamos las dos derivadas parciales:

Ahora, podemos comprobar que: 1) F(1,0) = 0. 2) F'(x,y) , F'(x,y) son continuas en un entorno del punto P(1,0). 3) F'(1,0) = -1 (distinta de 0). Por lo tanto cumple las condiciones de la función implícita, y según {3'} podemos expresar:

(válida para los puntos de un entorno de P(1,0) ).

Ahora obtenemos la segunda derivada, y", sin más que derivar esta y’, pero no olvidando que las y que aparecen en el numerador y denominadorson funciones de la forma y(x), no variables.

ahora tenemos que sustituir y' por el valor hallado anteriormente:

Una vez halladas y', y", podemos completar el estudio de y = y(x) hallando el valor de estas derivadas en el punto P(1,0):

El conocimiento de estas derivadas en P(1,0) nos posibilita hallar una aproximación a la función implícita y=f(x) sin más que tomar un desarrollo de Mc Laurin para esta función:

expresión válida en un entorno de P(1,0).

Función implícita de varias variables.

Lo que acabamos de ver para una función de una variable puede ser generalizado a una función de n variables de la siguiente manera.

Sea una ecuación con n+1 indeterminadas, en la forma F(x,y, ..., z) = 0 {4}, se dice que esta ecuación define en el entorno de un punto Po

a z=f(x,y,...) como una función implícita de n variables, si para todo punto P del entorno de Po se tiene que:

F(x,y,..., f(x,y,..))º 0.

* Teorema de existencia y unicidad:

Sea una ecuación de n+1 variables F(x,y,...,z) = 0 , esta ecuación define una función implícita z = f(x,y,...) en el entorno de un punto Po

si:

a) F

=0, es decir el punto Po satisface la ecuación.

b) Todas las derivadas parciales de F(x,y,...,z) :

, .... , son funciones continuas en el entorno del punto Po .

. Es decir, la derivada de F respecto de z no se anula.

Para obtener una expresión que nos dé las derivadas parciales de la función implícita, diferenciamos los dos miembros de la ecuación F(x,y,...,z) = 0 :

{5}

Ahora despejamos dz :

{6}

o expresado abreviadamente:

{6'}

y si tenemos en cuenta la expresión general de la diferencial de dz:

Podemos finalmente expresar las derivadas parciales de z:

{7}

Derivadas Direccionales

Se llaman derivadas direccional de la función z = f(x,y) en un punto P(x,y) en el sentido del vector

el siguiente límite si existe y es finito:

Para calcular este límite se toma el vector unitario

de la dirección del vector

(dividiéndolo por su módulo). Llamamos t a la longitud del vector

, es decir

,con lo cual

, de donde

, y el límite se reduce a la única variable t

Si la función f(x, y) es diferenciable, entonces la derivada direccional se calcula por la fórmula:

(es decir la suma de los productos de las parciales por las componentes del vector unitario)

Si la función es de tres variables z=f(x, y, z) la derivada direccional se calcula de manera análoga:

(Las parciales habrá que calcularlas en el punto correspondiente. Las componentes del vector unitario coinciden con los cosenos directores del vector director. Si la función no es diferenciable esta fórmula no es válida y hay que calcular el límite anterior).

Se llama gradiente de una función z = f(x, y) en un punto P(x, y) al vector que sale del punto P y sus componentes son las derivadas parciales de la función en dicho punto

La derivada direccional se puede obtener como el producto escalar del gradiente por el vector unitario (si la función es diferenciable)

El gradiente indica el sentido de crecimiento más rápido de una función en un punto dado. La derivada direccional tiene su valor máximo en el sentido del gradiente y coincide con su módulo:

Si la función es de tres variables u = f(x, y, z) el gradiente se define de forma análoga:

Planos tangentes a superficies de nivel

Si la superficie con ecuación F(x,y,z) = k es una superficie de nivel de 3 variables y sea P un punto de la superficie , C cualquier curva de la superficie que pase por el punto P
C = r(t)= (x(t), y(t), z(t)) t0 el valor del parámetro correspondiente a P: entonces r(t0) = (x0,y0,z0) como C esta en la superficie todo punto (X(t), y(t) , z(t)) debe satisfacer la ecuación de la superficie

F(x(t), y(t), z(t)) = k

entonces si x ,y y z son diferenciables se puede aplicar la regla de la cadena y queda de diez

y quedaría el vector gradiente por r'(t) = 0 para que sea un plano tangente

gradF . r'(t) = 0

entonces si t = t0

quedaría r(t0) = (x0,y0,z0)

y para el plano

gradF(x0,y0,z0) . r'(t0) = 0

traducido diríamos que el plano tangente a la superficie de nivel

F(x,y,z)=k en p(x0,y0,z0) osea que lo va a tocar en un solo punto en P y tiene como vector normal el plano gradiente de F (x0,y0,z0)

La ecuación del plano queda

Fx(x0,y0,z0) (x-x0)+Fy(x0,y0,z0) (y-y0)+Fz(x0,y0,z0) (z-z0) = 0

La dirección de la recta normal esta dada por el vector gradiente de F en (x0,y0,z0)

Por consiguiente las ecuaciones simétricas son

x-x0 = y-y0 = z-z0
Fx(x0,y0,z0) Fy(x0,y0,z0) Fz(x0,y0,z0)

y si es de dos variables F(x,y,z) = F(x,y) - z = 0 por que F(x,y) = z entonces lo paso para el otro lado y queda F(x,y)-z = 0

Máximos y Mínimos

Extremos relativos o locales

Si f es derivable en a, a es un extremo relativo o local si:
1. Si f'(a) = 0.
2. Si f''(a) ≠ 0

Máximos relativos o locales

Si f y f' son derivables en a, a es un máximo relativo si se cumple:
1. f'(a) = 0
2. f''(a) < 0

Mínimos relativos o locales

Si f y f' son derivables en a, a es un mínimo relativo si se cumple:

1. f'(a) = 0

2. f''(a) > 0

Cálculo de máximos y mínimos

1. Hallamos la derivada primera y calculamos sus raíces.

2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella las raíces de derivada primera y si:

f''(a) < 0 es un máximo relativo

f''(a) > 0 es un mínimo relativo

3. Calculamos la imagen (en la función) de los extremos relativos.

Ejemplo

f(x) = x³ − 3x + 2

f'(x) = 3x² − 3 = 0

f''(x) = 6x

f''(−1) = −6 Máximo

f''(1) = 6 Mínimo

f(−1) = (−1)³ − 3(−1) + 2 = 4

f(1) = (1)³ − 3(1) + 2 = 0

Máximo(−1, 4) Mínimo(1, 0)

Si ya hemos estudiado el crecimiento y decrecimiento de una función habrá:

1. Un máximo en el punto, de la función, en la que ésta pasa de creciente a decreciente.

2. Un mínimo en el punto, de la función, en la que ésta pasa de decreciente a creciente.

Ejemplo

Hallar los máximos y mínimos de:

Tenemos un mínimo en x = 3

Mínimo(3, 27/4)

En x = 1 no hay un máximo porque x = 1 no pertenece al dominio de la función.

Bibliografía:

http://teoremadelmes.blogspot.com/2008/04/planos-tangentes-superficies-de-nivel.html
http://www.ditutor.com/funciones_1/maximos_minimos.html
http://www.ehu.eus/juancarlos.gorostizaga/apoyo/func_implicit.htm
http://www.matap.uma.es/~svera/probres/pr3/pr3_4.html

JUEVES 11 DE JUNIO

Criterio de la segunda derivada

El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.

Se basa en el hecho de que si la gráfica de una función

f

es convexa en un intervalo abierto que contiene a

c

, y

f '(c)=0, f(c)

debe ser un mínimo relativo de

f

. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a

c

f '(c) = 0, f(c)

debe ser un máximo relativo de

f

Teorema

Sea $f$ una función tal que $f '(x) = 0$ y la segunda derivada de $f$ existe en un intervalo abierto que contiene a $x$

Si $f ''(x) < 0$ , entonces $f$ tiene un máximo relativo en $(x, f(x))$ .
Si $f ''(x) > 0$ , entonces $f$ tiene un mínimo relativo en $(x, f(x))$ .

f ''(x) = 0

, entonces el criterio falla. Esto es,

f

quizás tenga un máximo relativo en

x

, un mínimo relativo en

(x, f(x))

o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.

Máximos y Mínimos absolutos

EXTREMOS ABSOLUTOS (máximo y mínimo absolutos)

►El máximo absoluto es el mayor valor que alcanza la función en todo su dominio. Si existe, es único.
►El mínimo absoluto es el menor valor que alcanza la función en todo su dominio. Si existe, es único.

Los extremos absolutos pueden estar:
1º) En los extremos del dominio, si éste se definió como un intervalo cerrado.
2º) En los puntos del dominio donde la derivada primera vale cero.
3º) En los puntos del dominio donde la derivada primera no existe.

EJEMPLO. Hallar, si existen, los extremos absolutos de la función f(x) = x² + 3x en el intervalo [-2, 1]

SOLUCIÓN. La función tiene extremos absolutos si en el dominio que se definió es continua. Por ser una función polinómica, es continua en todo su dominio, en este caso, en [-2, 1].
Para hallar los extremos, evaluamos la función en los puntos antes mencionados.

1º) Extremos del dominio.
f(-2) = (-2)² + 3·(-2) = -2 ............................. ❶
f(1) = 1² + 3·1 = 4 ..................................... ❷

2º) Puntos donde f ' (x) = 0
f ' (x) = 2x + 3 = 0 ⇒ x = -3/2
Evaluamos la función en este punto:
f(-3/2) = (-3/2)² + 3·(-3/2) = -9/4 = -2,25.............................❸

3º) Puntos donde no existe f ' (x). Como f ' (x) es una función lineal, existe para cualquier valor de x. Entonces, en este caso no hay ningún punto.

Para determinar cuál es el máximo absoluto y el mínimo absoluto buscamos el valor mayor y el menor que toma la función en ❶ , ❷ y ❸.

RESPUESTA.
MÁXIMO ABSOLUTO = f(1) = 4
MÍNIMO ABSOLUTO = f(-3/2) = -9/4 = -2,25

Bibliografía:

https://es.wikipedia.org/wiki/Criterio_de_la_segunda_derivada
https://ar.answers.yahoo.com/question/index?qid=20091108114111AAGBgN5

LUNES 15 DE JUNIO

Máximos y Mínimos condicionados

Método de los multiplicadores de Lagrange.

Los extremos de la función f(x,y) condicionados por la restricción g(x,y)=0, se producen en los puntos críticos de la función de Lagrange:

Condiciones necesarias de extremo.

Las condiciones necesarias del extremo de una función de Lagrange vienen dadas por el sistema de ecuaciones.

Para resolver el sistema, eliminamos

de las dos primeras ecuaciones y el resultado lo sustituimos en la tercera (procurando no perder soluciones con las simplificaciones).

Condiciones suficientes para la existencia de extremos.

(a) Caso de dos variables.

Sea

un punto crítico de la función de Lagrange

, obtenido para un valor concreto

. Formamos la función de Lagrange para ese

Para estudiar su naturaleza podemos seguir dos caminos:

(a-1) Método de la diferencial segunda:

El problema de la existencia y el carácter del extremo condicional se resuelve averiguando el signo de la segunda diferencial de la función de Lagrange (particularizada para

)

a condición de que:

la función tiene un mínimo condicionado, y si

la función tiene un máximo condicionado.

Bibliografía:

http://www.matap.uma.es/~svera/probres/pr3/pr3a3_2.html

JUEVES18 DE JUINIO

Integrales Múltiples

Integrales Iteradas

Se llaman integrales iteradas a la realización sucesiva de por lo menos 2 procesos de integración simple considerando las diferenciales dx y dy.

Es importante tomar en cuenta en que posición vienen dados los límites de las integrales en cuestión para saber en que orden serán ejecutados los procesos de integración simple; es decir, reconocer si se va integrar primero considerando la diferencial dx o la diferencial dy o viceversa.

FORMAS EN QUE PUEDEN PRESENTARSE LAS INTEGRALES ITERADAS

Área por Doble Integración

La aplicación más simple de las integrales dobles es para hallar el área de una región del plano xy. Esta área esta dada por una cualquiera de las integrales

Los límites de integración apropiados. Ya hemos visto como se hace esto en la figura 1, cuando se efectúan las integraciones primero respecto a y, y después respecto a x; es decir

Esta última integral podía haberse escrito de primera intención, puesto que expresa el área como límite de la suma de fajas horizontales.

Integrales dobles como volúmenes

Cuando f(x ,y) es positiva podemos interpretar la integral doble de f sobre una región rectangular R como el volumen del prisma sólido limitado abajo por R y arriba por la superficie z = F(x, y). Cada termino f (xk, yk)

"Ak en la suma Sn = Monografias.com

"Ak es el volumen de un prisma rectangular vertical que aproxima el volumen de la porción del sólido que está directamente arriba de la base "Ak. La suma Sn aproxima entonces a lo que llamamos volumen total del sólido. Definido este volumen como

Coordenadas Polares

En un espacio R2, un dominio de integración que tenga una simetría circular es muchas veces suceptible de ser transformado de coordenadas rectangulares a polares, lo que significa que cada punto P (x, y) del dominio de una integral doble tomará su valor correspondiente en coordenadas polares mediante la siguiente transformación:

Por ejemplo:

Si aplica la identidad trigonométrica pitagórica de senos y cosenos.

El determinante jacobiano de la transformación es:

Definición Integral triple

Es la aplicación sucesiva de tres procesos de integración definida simple a una función de tres variables f (x, y, z); tomando en consideración en función de que variable se encuentran los límites para saber cual diferencial (dx, dy, dz) se utilizará primero y cual después y cual al final.

Ejemplo.

Integrales Triples en Coordenadas Cilíndricas y Esféricas

Coordenadas cilíndricas.

Las coordenadas cilíndricas son apropiadas para describir cilindros cuyos ejes coinciden con el eje x y planos que contienen el eje z o bien son perpendiculares a el.

r = 4 Cilindro, radio 4, eje el eje z

Plano que contiene al eje z

z= 2 Plano perpendicular al eje z

El elemento de volumen para subdividir una región en el espacio con coordenadas cilíndricas es

Las integrales triples en coordenadas cilíndricas son entonces evaluadas como integrales iteradas, como el siguiente ejemplo.

EJEMPLO.

Solución

Paso 1: La base de D también es la proyección de la región R sobre el plano xy. La frontera de R es el

círculo

Su ecuación en coordenadas polares es

Paso 2: Los límites z de integración. Una recta M, que pasa por un punto típico (r, ) en R, paralela al eje z, entra a D en z=0 y sale en

Paso 3: Los límites r de integración. Un rayo L que pasa por (r, ) desde el origen, entra a R en r =0 y sale en

Paso 4: Los límites de integración. Al barrer L a través de R, el ángulo que forma con el eje x positivo varía de La integral es

Coordenadas esféricas.

Las coordenadas esféricas son apropiadas para describir con centro en el origen, medios planos articulados a lo largo de eje z y conos simples, cuyos vértices se encuentran en el origen, y con ejes a lo largo del eje z.

Las superficies como ésas tienen ecuaciones de valor coordenado constante:

EJEMPLO.

El volumen es

Bibliografía:

http://www.monografias.com/trabajos83/integrales-multiples/integrales-multiples2.shtml

LUNES 22 DE JUNIO

Resolución de ejercicios con integrales simples, dobles y triples.

INTEGRALES DOBLES SOBRE RECTANGULOS.

Suponga que f(x, y) está definida sobre una región rectangular R dada por

R: a<x<b, c<y<d.

Imaginamos R cubierta por una red de rectas paralelas a los ejes x y y. Esas rectas dividen R en pequeños elementos de área "A1, "A2…, "An, escogemos un punto (xk, yp) en cada elemento "Ak y formamos la suma

Si f es continua en toda la legión R, entonces al refinar el ancho de la red para hacer tender "x, "y a cero, las sumas en (1) tienden a un límite llamado integral doble de f sobre R. Su notación es

Entonces,

Igual que en las funciones de una sola variable, las sumas tiende a este límite independientemente de cómo se subdividan los intervalos [a, b] y [c, d] que determinan R, siempre que las normas de las subdivisiones tiendan ambas a cero. El límite (2) también es independiente del orden en que se numeren las áreas "Ak e independiente de la selección del punto (xk, yk) dentro de cada "Ak. Los valores de las sumas aproximadas individuales Sn depende de esas selecciones, pero al final las sumas tienden al mismo límite. La prueba de la existencia y unicidad de este límite para una función continua f se da en textos más avanzados.

La continuidad de f es una condición suficiente para la existencia de la integral doble, pero no es una condición suficiente para la existencia de la integral doble, pero no es una condición necesaria. El límite en consideración también existe para muchas funciones discontinuas.

PROPIEDADES DE LAS INTEGRALES DOBLES.

Las integrales dobles de funciones continuas tienen propiedades algebraicas que son útiles en los cálculos y en las aplicaciones.

Esta propiedad es válida cuando R es la unión de dos rectángulos R1 y R2 que no se traslapan.

INTEGRALES DOBLES COMO VOLUMENES.

Cuando f(x ,y) es positiva podemos interpretar la integral doble de f sobre una región rectangular R como el volumen del prisma sólido limitado abajo por R y arriba por la superficie z = F(x, y). Cada termino f (xk, yk) "Ak en la suma Sn =

INTEGRALES DOBLES SOBRE REGIONES ACOTADAS NO RECTANGULARES.

Para definir la integral doble de una función f(x, y) sobre una región acotada no rectangular, imaginamos de nuevo R cubierta por una retícula rectangular, pero incluimos en la suma parcial sólo las pequeñas piezas de área "A = "x"y que se encuentran totalmente dentro de la región. Numeramos las piezas en algún orden, escogemos un punto arbitrario (xk, yk) en cada "Ak y formamos la suma

La única diferencia entre esta suma y la de la ecuación (1) para regiones rectangulares es que ahora las áreas "Ak pueden dejar de cubrir toda R. Pero conforme la red se vuelve más fina y el número de términos en Sn aumenta, más de R queda incluida. Si f es continua y la frontera de R está hecha de las gráficas de un número finito de funciones continuas de xy/o de y, unidas extremo con extremo, entonces las sumas Sn tendrán un límite cuando las normas de las subdivisiones que definen la malla rectangular tiendan independientemente a cero. Llamamos al límite integral doble de f sobre R.

Este límite también puede existir en circunstancias menos restrictivas.

Las integrales dobles de funciones continuas sobre regiones no rectangulares tienen las mismas propiedades algebraicas que las integrales sobre regiones rectangulares. La propiedad de aditividad de dominio correspondiente a la propiedad 5 dice que si R se descompone en regiones no traslapadas R1 y R2 con fronteras que están nuevamente hechas de un número finito de segmentos de rectas o curvas, entonces

Si R es una región limitada “arriba” y “abajo” por las curvas y=g2(x) y y=g1(x) y lateralmente por las rectas x=a, x=b, nuevamente podemos calcular el volumen por el método de rebanadas. Primero determinamos el área de la sección transversal

Y luego integramos A(x) de x=a a x=b para obtener el volumen como una integral iterada:

(8)

De manera similar, si R es una región, limitada por las curvas x=h2 (y) y x=h1 (y) y las rectas y=c y y=d, entonces el volumen calculado por el método de rebanadas está dado por la integral iterada

EJEMPLO. Encuentre el volumen del prisma cuya base es el triángulo en el plano xy limitado por el eje x y las rectas y=x y x=1, y cuya parte superior se encuentra en el plano

z=f(x, y)=3-x-y.

Solución. Para cualquier x entre 0 y 1, y puede variar de y=0 a y=x. Por consiguiente.

INTEGRALES TRIPLES EN COORDENADAS RECTANGULARES.

Usamos integrales triples para hallar los volúmenes de formas tridimensionales, la masa y los momentos de sólidos y los valores promedio de funciones de tres variables.

INTEGRALES TRIPLES.

Si F(x, y, z) es una función definida sobre una región D cerrada en el espacio, por ejemplo, la región ocupada por una bola sólida o una masa de arcilla, entonces la integral de F sobre D puede definirse de la siguiente manera. Subdividimos una región rectangular que contenga a D en celdas rectangulares por planos paralelos a los planos coordenados. Las celdas que se encuentran dentro de D de 1 a n en cierto orden; una celda típica tendrán entonces dimensiones "xk por "yk por "zk y volumen "x"xk. Escogemos un punto (xk, yk, zk) en cada celda y formamos la suma

Si F es continua y la superficie que limita a D está hecha de superficies suaves unidas a lo largo de curvas continúas, entonces cuando "xk, "yk, "zk tienden a cero independientemente, las sumas Sn tenderán a un límite

Llamamos a este límite integral triple de F sobre D. El límite también existe par algunas funciones discontinuas

Bibliografía:

http://html.rincondelvago.com/integrales-multiples.html

JUEVES 25 DE JUNIO

Centros de masa

Distribución discreta de materia

Para un sistema de masas discreto, formado por un conjunto de masas puntuales, el centro de masas se puede calcular como:

$\mathbf r_{\text{cm}}=\frac{\sum_i m_i\mathbf r_i}{\sum_i m_i}=\frac{1}{M}\sum_i m_i\mathbf r_i$

M

, masa total del sistema de partículas.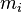

m_i\,

, masa de la partícula i-ésima.

\mathbf {r}_i

, vector de posición de la masa i-ésima respecto al sistema de referencia supuesto.

Un poco más explícito si A₁,... A_n son n puntos, y m₁,... m_n n números (m como masa). Entonces el centro de masa de los (A_i, m_i) es el punto Gdefinido como sigue:

$\overrightarrow{OG\,} = \frac{\sum{m_i\overrightarrow{O\!A_i}}}{\sum{m_i}} = \frac{m_1\overrightarrow{O\!A_1} + ...+m_n\overrightarrow{O\!A_n}} {m_1+...+m_n}, \quad \mbox{con} \quad \sum{m_i} \ne 0$

Esta definición no depende del punto O, que puede ser cualquiera. Si se toma el origen del plano o del espacio, se obtienen las coordenadas del baricentro como promedio ponderado por los m_i de las coordenadas de los puntos A_i:

$\mathbf{r}_{\text{cm}} = \mathbf{r}_G= \frac{\sum{m_i\mathbf{r}_i}}{\sum{m_i}}= \frac{m_1\mathbf{r}_1+\dots+m_n\mathbf{r}_n}{m_1+\dots+m_n}$

La definición anterior equivale a la fórmula siguiente, más práctica para el cálculo vectorial, pues prescinde de las fracciones (se obtiene tomando O =G):

$\sum_{i=1}^n{m_i\overrightarrow{G\!A_i}} = \vec 0 \quad \mbox{o bien} \quad m_1\overrightarrow{G\!A_1} + ...+m_n\overrightarrow{G\!A_n} = \vec 0$

Distribución cuasidiscreta de materia

En el caso de un sistema de cuerpos cuasipuntuales, o cuerpos que distan entre sí mucho más que las dimensiones de cada uno de los cuerpos, el cálculo anterior resulta bastante aproximado.

Distribución continua de materia

Para sistemas de masas continuos o distribuciones continuas de materia debemos recurrir al Cálculo Infinitesimal e Integral, de modo que la expresión anterior se escribe en la forma:

$\mathbf r_{\text{cm}} = \frac{\int\mathbf r \ dm}{\int dm} = \frac{1}{M}\int\mathbf r \ dm$

Distribución de masa homogénea: Si la masa está distribuida homogéneamente, la densidad será constante por lo que se puede sacar fuera de la integral haciendo uso de la relación siguiente: $dm = \rho \ dV$

$\mathbf r_{\text{cm}} = \frac{\rho \int_V \mathbf r \ dV}{\rho \int \ dV} = \frac{\int_V \mathbf r \ dV}{V}$

siendo V el volumen total.

Para cuerpos bidimensionales (superficies) o monodimensionales (líneas) se trabajará con densidades superficiales y longitudinales respectivamente.

Para el caso de cuerpos con densidad uniforme, el c.m. coincidirá con el centroide del cuerpo.

Distribución de masa no homogénea: Los centros de masas en cuerpos de densidad variable pueden calcularse si se conoce la función de densidad $\rho (\mathbf r)$ . En este caso se calcula el centro de masas de la siguiente forma.

$\mathbf r_\text{cm}= \frac{\int_V \mathbf r \ \rho (\mathbf {r}) \ dV}{M}$

Para calcular la integral hay que conocer la función de densidad.

Momentos de Inercia

Dado un sistema de partículas y un eje arbitrario, el momento de inercia del mismo se define como la suma de los productos de las masas de las partículas por el cuadrado de la distancia r de cada partícula a dicho eje. Matemáticamente se expresa como:

$I = \sum m_ir_i^2 \,$

Para un cuerpo de masa continua (Medio continuo), se generaliza como:

$I = \int_m r^2 dm = \int_V \rho r^2 \,dV$

El subíndice V de la integral indica que se integra sobre todo el volumen del cuerpo. Se resuelve a través de una integral triple.

Este concepto desempeña en el movimiento de rotación un papel análogo al de masa inercial en el caso del movimiento rectilíneo y uniforme. La masa inercial es la resistencia que presenta un cuerpo a ser acelerado en traslación y el Momento de Inercia es la resistencia que presenta un cuerpo a ser acelerado en rotación. Así, por ejemplo, la segunda ley de Newton:

\scriptstyle{F = m a}

tiene como equivalente para la rotación:

\tau = I \alpha\,

donde:

$\scriptstyle{\tau}$ es el momento aplicado al cuerpo.
$\scriptstyle{I}$ es el momento de inercia del cuerpo con respecto al eje de rotación y
$\textstyle{\alpha={d^2\theta\over dt^2}}$ es la aceleración angular.

Siempre y cuando la distancia con respecto al sistema de referencia permanezca constante.

La energía cinética de un cuerpo en movimiento con velocidad v es

\scriptstyle{{1\over 2}mv^2}

, mientras que la energía cinética de un cuerpo en rotación con velocidad angular ω es

\scriptstyle{{1\over 2}I\omega^2}

, donde

I

es el momento de inercia con respecto al eje de rotación.

La conservación de la cantidad de movimiento o momento lineal tiene por equivalente la conservación del momento angular

\scriptstyle{\vec L}

\vec L = I\vec \omega

El vector momento angular, en general, no tiene la misma dirección que el vector velocidad angular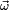

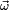\scriptstyle{\vec \omega}

. Ambos vectores tienen la misma dirección si el eje de giro es un eje principal de inercia. Cuando un eje es de simetría entonces es eje principal de inercia y entonces un giro alrededor de ese eje conduce a un momento angular dirigido también a lo largo de ese eje.

Teorema de Steiner o teorema de los ejes paralelos

Artículo principal: Teorema de Steiner

El teorema de Steiner (denominado en honor de Jakob Steiner) establece que el momento de inercia con respecto a cualquier eje paralelo a un eje que pasa por el centro de masa, es igual al momento de inercia con respecto al eje que pasa por el centro de masa más el producto de la masa por el cuadrado de la distancia entre los dos ejes:

I_{eje} = I_{eje}^{(CM)} + Mh^2 \,

donde: I_eje es el momento de inercia respecto al eje que no pasa por el centro de masa; I^(CM)_eje es el momento de inercia para un eje paralelo al anterior que pasa por el centro de masa; M (Masa Total) y h (Distancia entre los dos ejes paralelos considerados).

La demostración de este teorema resulta inmediata si se considera la descomposición de coordenadas relativa al centro de masas C

\bar{\mathbf{r}} = \mathbf{r}_{C} + \mathbf{h}

inmediata:

I_{eje} = \int_V \bar{\mathbf{r}} \cdot \bar{\mathbf{r}} \quad dm = \int_V (\mathbf{r}_{C}\cdot\mathbf{r}_{C}+2\mathbf{r}_{C}\cdot\mathbf{h}+ \mathbf{h}\cdot\mathbf{h}) \quad dm = \int_V \mathbf{r}_{C}\cdot\mathbf{r}_{C} \quad dm + \int_V 2\mathbf{r}_{C}\cdot\mathbf{h} \quad dm + \int_V \mathbf{h}\cdot\mathbf{h} \quad dm

I_{eje} = I_{eje}^{(CM)} + \underbrace{2\mathbf{h}\cdot\int_V \mathbf{r}_{C} dm}_{=0} + Mh^2

donde el segundo término es nulo puesto que la distancia vectorial promedio de masa en torno al centro de masa es nula, por la propia definición de centro de masa.

El centro de gravedad y el centro de masa pueden no ser coincidentes, dado que el centro de masa sólo depende de la geometría del cuerpo, en cambio, el centro de gravedad depende del campo gravitacional en el que está inmerso dicho cuerpo.

Bibliografía:

https://es.wikipedia.org/wiki/Centro_de_masas
https://es.wikipedia.org/wiki/Momento_de_inercia

LUNES 29 DE JUNIO

Campo Vectorial

Campos vectoriales. Un campo vectorial es en Rn es una aplicación F:ARn → Rn que asigna a cada punto x de su dominio A un vector F (x). Si n = 2, F se llama campo vectorial en el plano, y si n = 3, F es un campo vectoriales del espacio.

Visualizar F adhiriendo una flecha a cada punto (Fig. 4.3.1). En contraste, una aplicación f:A Rn → R que asigna un número a cada punto es un campo escalar. Un campo vectorial F (x,y,z) en R3 tiene tres campos escalares componentes F1, F2 y F3, así que

F(x, y, z) = (F1(x, y, z), F2(x, y, z), F3(x, y, z)).

De manera análoga, un campo vectorial Rn tiene n componentes F1, ..., Fn. Si cada componente es una función Ck, decimos que el campo vectorial F es de clase Ck. Se dará por hecho que los campos vectoriales son, al menos, de clase C1, a no ser que se diga lo contrario.

Figura 4.3.1 Un campo vectorial F asigna un vector F (x) a cada punto x de su dominio.

Ejemplo 1
Realizar la descripción del campo vectorial F dado por F (x, y) = -yi + xj.

Solución
La siguiente tabla muestra los sectores F (x, y) asociados a varios puntos (x, y) señalados en la figura 18.5.

(x, y)	F(x, y)
(1,3)	- 3i +j
(-3,1)	-i – 3j
(-1, -3)	3i - j
(3,-1)	i + 3j
(x, y)	F(x, y)
(1,1)	- i +j
(-1,1)	-i - j
(-1, -1)	i - j
(1,-1)	i + j

Figura 18.5 Figura 18.6

Para llegar a una descripción de un campo vectorial F se considera un punto arbitrario K (x, y) y se define el vector de posición r = xi + yj de K (x, y) (véase la figura 18.6). Se ve que F (x, y) es ortogonal a r y por lo tanto, es tangente a la circunferencia de radio ||r|| con centro en el origen. Este hecho puede demostrarse probando que r . F (x, y) = 0, como sigue:

r . F (x, y) = (xi + yj) . (- yi +xj)

= -xy + yx = 0.

Además,

|| F (x, y) || = √y2 + x2 = || r ||

Por lo tanto, la magnitud de F (x, y) es igual al radio de la circunferencia. Esto implica que cuando el punto K (x, y) se aleja del origen, la magnitud de F (x, y) aumenta como sucede en el caso de la rueda giratoria de la figura 18.1

La siguiente definición presenta uno de los campos vectoriales más importantes de la física.
Definición (18.2).

Sea r = xi + yj + zk el vector posición de un punto K (x, y, z). Se dice que un campo vectorial F es un campo de variación inversa al cuadrado de la distancia si

F(x, y, z) = c_ u

|| r ||2

donde c es un escalar y u es un vector unitario que tiene la misma dirección que r y está dado por u = 1_ = r.

|| r ||

Ejemplo 2

Describir el campo F (x, y, z) que cumple la definición (18.2) para c < 0.

Solución

Como u = 1 r y r = xi + yj + zk,

||r||

F (x, y, z) = c_ r = c_____ (xi + yj + zk).

||r||3 (x2 + y2 + z2)3/2

Es más fácil analizar los sectores del campo usando la expresión en términos de r. Como F(x, y, z) es un múltiplo escalar negativo de r, la dirección de F(x, y, z) es hacia el origen O. Además,

||F(x, y, z)|| = | c |_ || u || = | c |_

||r||2 ||r||2

y por lo tanto, la magnitud de F (x, y, z) es inversamente proporcional al cuadrado de la distancia del punto (x, y, z) al origen O. Esto significa que cuando el punto K(x, y, z) se aleja del origen, la longitud del vector asociado F (x, y, z) disminuye.

En la figura 18.7 se indican algunos vectores típicos de un campo F del tipo de "variación inversa al cuadrado".

Definición

Se dice que un campo vectorial F es un campo vectorial conservativo si es el gradiente de una función escalar, es decir si

F (x, y, z) = s f (x, y, z)

para una función f.

Teorema

Todo campo vectorial del tipo de variación inversa al cuadrado (o de tipo gravitacional) es conservativo.

Demostración. Si F es un campo de tipo gravitacional, entonces como en la solución del ejemplo 2,

F(x, y, z) = cx____ i + cy____ j + cz____ k

(x2 + y2 + z2)3/2 (x2 + y2 + z2)3/2 (x2 + y2 + z2)3/2

para alguna constante c. Según la definición (18.3, si F es conservativo, existe una función escalar f tal que F (x, y, z) = s f (x, y, z), y las componentes de F son iguales a fx (x, y, z), fy (x, y, z) y fz (x, y, z), respectivamente. Integrando parcialmente estas componentes con respecto a x, y y z, respectivamente, se ve que

f(x, y, z) = – c_____

(x2 + y2 + z2)1/2

Calculando las derivadas parciales se demuestra que esta función f es lo que se buscaba. Por tanto, se tiene lo siguiente:

F(x, y, z) = s f (x, y, z) = s -c donde r = || r || (x2 + y2 + z2)1/2

En la física, la función de potencial de un campo vectorial conservativo F se define como una función p tal que F(x, y, z) = -s p (x, y, z). En este caso, tomando p = -f en la demostración del teorema (18.4), se obtiene F(x, y, z) = s (c/r).

Más adelante en el capítulo se estudiarán más a fondo los campos vectoriales conservativos.
El operador diferencial vectorial s en tres dimensiones es:

s = i ∂_ + j ∂_ + k ∂_

∂x ∂y ∂z

Si s actúa sobre una función escalar f, da como resultado el gradiente de f:

grad f =s f = ∂f_ i + ∂f_ j + ∂f_ k

∂x ∂y ∂z

Aplicaciones del campo vectorial

Un campo vectorial en Rⁿ es una aplicación:

F: A d Rⁿ à Rⁿ

Que asigna a cada punto x de su dominio A un vector F(x).

Si n = 2, F se denomina un campo vectorial en el plano.

Si n = 3, F es un campo vectorial en el espacio.

Podemos representar F dibujando una flecha en cada punto.

Utilizaremos el programa Maple en la representación de campos vectoriales

Ejemplo 1.- Dibujar varios vectores representativos del campo:

F(x,y) = ( ½ xy , ¼ x²)

Solución:

Figura 2.1.1.- Vectores en el plano representativos del campo vectorial F(x,y) = ( ½ xy , ¼ x²)

Ejemplo 2.- Dibujar varios vectores representativos del campo:

F(x , y, z) = ( 2x , 2y , z)

Solución:

Figura 2.1.2.- Vectores en el espacio representativos del campo vectorial F(x , y, z) = ( 2x , 2y , z)

En muchas aplicaciones el vector F(x) representa una cantidad física (fuerza, velocidad, etc.) asociada con la posición x.

Integrales de Línea

Integral curvilínea de un campo escalar

\int_C f\ ds = \int_a^b f(\mathbf{r}(t)) \|\mathbf{r}'(t)\|\, dt = \int_a^b f(\mathbf{x}(t),\mathbf{y}(t))\sqrt{[\mathbf{x}'(t)]^2+[\mathbf{y}'(t)]^2 }dt

Para f : R² → R un campo escalar, la integral sobre la curva C (también llamada, integral de trayectoria), parametrizada como r(t)=x(t)i+y(t)j con t

\in

[a, b], está definida como:

donde: r: [a, b] → C es una parametrización biyectiva arbitraria de la curva C de tal manera que r(a) y r(b) son los puntos finales de C. Las integrales de trayectoria son independientes de la parametrización r(t), porque solo depende de la longitud del arco, también son independientes de la dirección de la parametrización r(t).

Integral curvilínea de un campo vectorial

Para F : Rⁿ → Rⁿ un campo vectorial, la integral de línea sobre la curva C, parametrizada como r(t) con t

\in

[a, b], está definida como:

\int_C \mathbf{F}(\mathbf{r})\cdot\,d\mathbf{r} = \int_a^b \mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt.

donde

\cdot

es el producto escalar y r: [a, b] → C es una parametrización biyectiva arbitraria de la curva C de tal manera que r(a) y r(b) son los puntos finales de C.

Las integrales de línea de un campo vectorial son independientes de la parametrización siempre y cuando las distintas parametrizaciones mantengan el sentido del recorrido de la curva. En caso de elegirse dos parametrizaciones con sentidos de recorrido contrarios, las integrales de línea del mismo campo vectorial resultarán con iguales módulos y signos contrarios.

Otra forma de visualizar esta construcción es considerar que

\int_C \mathbf{F}(\mathbf{x})\cdot\,d\mathbf{x} = \int_C \mathbf{F}_1 dx^1+\mathbf{F}_2 dx^2+\cdots+\mathbf{F}_n dx^n

donde se aprecia que la integral de línea es un operador que asigna un número real al par

(C,\mathbf{\omega})

donde

\mathbf{\omega}=\mathbf{F}_1 dx^1+\mathbf{F}_2 dx^2+\cdots+\mathbf{F}_n dx^n

es una 1-forma.

Independencia de la curva de integración

Si el campo vectorial F es el gradiente de un campo escalar G (o sea, si el campo vectorial F es conservativo), esto es:

\nabla G = \mathbf{F},

entonces la derivada de la función composición de G y r(t) es:

\frac{dG(\mathbf{r}(t))}{dt} = \nabla G(\mathbf{r}(t)) \cdot \mathbf{r}'(t) = \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}'(t)

con lo cual, evaluamos la integral de línea de esta manera:

\int_C \mathbf{F}(\mathbf{x})\cdot\,d\mathbf{x} = \int_a^b \mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt = \int_a^b \frac{dG(\mathbf{r}(t))}{dt}\,dt = G(\mathbf{r}(b)) - G(\mathbf{r}(a)).

La integral de F sobre C depende solamente de los valores en los puntos r(b) y r(a) y es independiente del camino entre a y b.

Por esta razón, un campo vectorial que es el gradiente de un campo escalar, es llamado independiente del camino o también conservativo. Cabe destacar que si tenemos un campo arbitrario; tal que, las derivadas parciales iteradas sean iguales y además sea convexo; entonces este campo es el gradiente de una función potencial φ. Y por lo mencionado anteriormente la integral de línea del campo es independiente del camino.

Bibliografía:

http://www.monografias.com/trabajos14/camposvectoriales/camposvectoriales.shtml
http://fcm.ens.uabc.mx/~chelo/analisis%20vectorial/nucleos/capitulo2/l2_1.htm
https://es.wikipedia.org/wiki/Integral_de_l%C3%ADnea

Inicio

sábado, 11 de abril de 2015

Inicio

jueves, 9 de abril de 2015

Evidencias

Julio

Junio

Mínimos relativos o locales

Si f y f' son derivables en a, a es un mínimo relativo si se cumple:

1. f'(a) = 0

2. f''(a) > 0

Cálculo de máximos y mínimos

1. Hallamos la derivada primera y calculamos sus raíces.

2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella las raíces de derivada primera y si:

f''(a) < 0 es un máximo relativo

f''(a) > 0 es un mínimo relativo

3. Calculamos la imagen (en la función) de los extremos relativos.

Ejemplo

f(x) = x3 − 3x + 2

f'(x) = 3x2 − 3 = 0

f''(x) = 6x

f''(−1) = −6 Máximo

f''(1) = 6 Mínimo

f(−1) = (−1)3 − 3(−1) + 2 = 4

f(1) = (1)3 − 3(1) + 2 = 0

Máximo(−1, 4) Mínimo(1, 0)

Si ya hemos estudiado el crecimiento y decrecimiento de una función habrá:

1. Un máximo en el punto, de la función, en la que ésta pasa de creciente a decreciente.

2. Un mínimo en el punto, de la función, en la que ésta pasa de decreciente a creciente.

Ejemplo

Hallar los máximos y mínimos de:

Tenemos un mínimo en x = 3

Mínimo(3, 27/4)

En x = 1 no hay un máximo porque x = 1 no pertenece al dominio de la función.

Integrales Iteradas

Área por Doble Integración

Integrales dobles como volúmenes

Coordenadas Polares

Definición Integral triple

Integrales Triples en Coordenadas Cilíndricas y Esféricas

Distribución cuasidiscreta de materia

Distribución continua de materia

Teorema de Steiner o teorema de los ejes paralelos

Integral curvilínea de un campo escalar

Integral curvilínea de un campo vectorial

Independencia de la curva de integración

f(x) = x³ − 3x + 2

f'(x) = 3x² − 3 = 0

f(−1) = (−1)³ − 3(−1) + 2 = 4

f(1) = (1)³ − 3(1) + 2 = 0